Іванченко Дар’я
Науковий керівник: Шевченко Н.Г.
Кіровоградський державний педагогічний університет імені Володимира Винниченка
Анотація: В роботі розглядаються та аналізується залежність між змінами в динаміці розміру середньої щомісячної заробітної плати в Україні та динаміки індексу інфляції за різними регресійними моделями. Прогнозовано розмір середньої заробітної плати в Україні на 6 місяців за двома способами. Проведено порівняльний аналіз побудованих моделей та прогнозів.
Ключові слова: статистика, індекс інфляції, заробітна плата, МНК, панельні дані, фіксовані ефекти, регресійний аналіз, прогноз.
Заробітна плата як показник, є не лише індикатором, що визначає загальний життєвий рівень працівників. Від її стану та форм реалізації, частки у ВНП багато в чому залежать також можливості розвитку економіки взагалі. В умовах сучасного ринкового механізму, заробітна плата стає дедалі вагомішим чинником відтворення суспільного виробництва. Цей показник виступає як один із основних регулювальників ринку праці. Однак аналізу і оцінці впливу зарплат на ринок праці й, передусім, на зайнятість в Україні не приділяється належна увага, що призводить до негативних наслідків – прискореного зростання безробіття, руйнування мотивів і стимулів до праці та ін..
Мета роботи: дослідити вплив індексу споживчих цін (інфляцїї) на розмір середньої заробітної плати за місяць в Україні за різними регресійними моделями. Проаналізувати отримані моделі. Розрахувати прогноз за найбільш точною моделлю та за методом експоненційного згладжування, проаналізувати та порівняти отримані результати.
Для проведення дослідження було використано щомісячну статистичну інформацію за період від січня 2014 р. по вересень 2016 р., що характеризує залежність середньої заробітної плати за місяць в Україні (в розрахунку на одного штатного працівника, грн.) від динаміки індексу споживчих цін (у відсотках). Вхідні дані можна графічно побачити на рис.1.
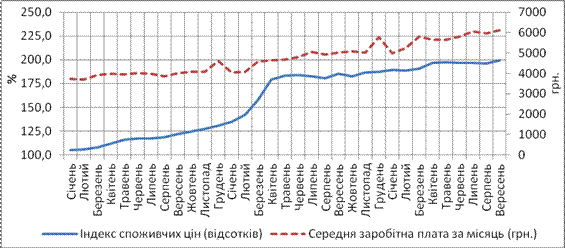
Рис. 1. Динаміка змін середньої заробітної плати за місяць та індексу споживчих цін
На даному графіку досить добре прослідковується синхронність обох ознак, що може вказувати на прямий зв’язок між ними.
За наявними даними спостережень в MS Office Excel було побудовано та порівняно наступні регресійні моделі:
- Лінійна регресійна модель, вигляд якої
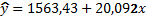 ;
; - Нелінійні регресійні моделі:
- Степенева:
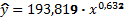 ;
; - Експоненціальна:
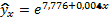 ;
; - Напівлогарифмічна:
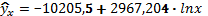 ;
; - Гіперболічна:
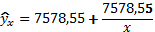 ;
; - Обернена
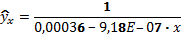 .
.
Табл. 1
Зведена таблиця результатів
| Модель | Коефіцієнт кореляції
| Коефіцієнт детермінації ( | Середня похибка апроксимації (A) | F | Fтабл | |
| Лінійна | 0,918 | 0,843 | 4,89% | 166,738 | > | 4,1596 |
| Степенева | 0,913 | 0,834 | 4,97% | 155,659 | > | |
| Експоненціальна | 0,925 | 0,857 | 4,51% | 185,139 | > | |
| Напівлогарифмічна | 0,905 | 0,819 | 5,46% | 140,792 | > | |
| Гіперболічна | 0,89 | 0,792 | 6,01% | 117,981 | > | |
| Обернена | 0,932 | 0,869 | 4,22% | 204,871 | > |
Для кожної моделі було розраховано коефіцієнт кореляції (для оцінки тісноти зв’язку між ознаками), коефіцієнт детермінації (для оцінки якості моделі), середня помилка апроксимації, оцінку значущості рівняння регресії (за допомогою критерію Фішера). Отримані результати наведено табл. 1.
Згідно з отриманими результатами, всі моделі є статистично значущими і добре описують дані спостережень, але серед парних регресій, залежність між ознаками найкраще описує обернена регресійна модель. Про це свідчить те, що вона має найбільші коефіцієнт кореляції (0,932) та коефіцієнт детермінації (0,869), а отже і найменшу похибку апроксимації (4,22%).
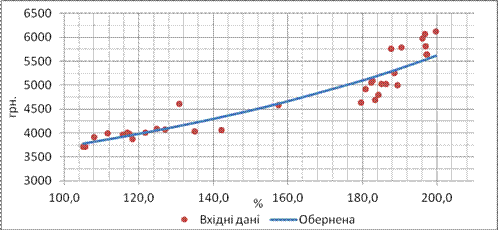
Рис. 2. Графік оберненої регресії та вхідних даних
Було також побудовано та досліджено регресійну модель з фіксованими ефектами на основі панельних даних, вигляд якої:
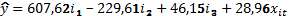
Для побудови цієї моделі вводилися 3 фіктивних змінних за формулою [2, с.10]: 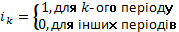
Це дозволить простежити та проаналізувати вплив фактора X на залежну ознаку Y за кожний окремий період (в нашому випадку періодом є рік). Аналізуючи коефіцієнти при фіктивних змінних, можна зробити висновок, що найсильнішим вплив був у 2014 р. (i1).
Для цієї моделі коефіцієнт кореляції 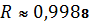 , коефіцієнт детермінації
, коефіцієнт детермінації 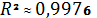 є близьким до одиниці, що свідчить про достовірність отриманої моделі. Для перевірки значущості фіксованих ефектів, було обчислено значення F-статистики. У нашому випадку , тому гіпотеза про рівність всіх індивідуальних ефектів відхиляється. Отже, побудована модель є правомірною, а гіпотеза про вплив індексу споживчих цін (інфляції) на розмір середньої заробітної плати за місяць в Україні підтверджується.
є близьким до одиниці, що свідчить про достовірність отриманої моделі. Для перевірки значущості фіксованих ефектів, було обчислено значення F-статистики. У нашому випадку , тому гіпотеза про рівність всіх індивідуальних ефектів відхиляється. Отже, побудована модель є правомірною, а гіпотеза про вплив індексу споживчих цін (інфляції) на розмір середньої заробітної плати за місяць в Україні підтверджується.
Порівнюючи обернену модель та модель панельних даних з фіксованими ефектами, можна стверджувати, що остання є ще більш точнішою. На це вказує більші значення 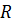 та
та 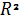 , та менша похибка апроксимації цієї моделі (3,6%).
, та менша похибка апроксимації цієї моделі (3,6%).
Було розраховано прогноз розміру середньої заробітної плати за місяць в Україні на наступні 6 місяців за моделлю та за методом експоненційного згладжування. Для розрахунку прогнозу за оберненою парною моделлю (яка найбільш точніше описує дані спостережень), спочатку було знайдено прогнозні значення незалежної змінної.
Рис. 3. Порівняння прогнозів розміру середньої заробітної плати в Україні
Порівнюючи обидва методи, можна стверджувати, що результати прогнозування мають незначну розбіжність в перші 2 місяці прогнозу, та відносно невелика розбіжність результатів має місце у наступні 4 місяці. Обернена регресія дає більш прогресуючий прогноз. В цілому, отримані результати показують однакову тенденцію змін.
Згідно з результатами дослідження, можна зробити висновок, що залежність між індексом споживчих цін та розміром середньої заробітної платив Україні є дуже сильною та прямою, тобто із збільшенням першої ознаки збільшується й друга. Згідно з результатами прогнозу, розмір середньої заробітної плати в Україні в наступні 6 місяців буде збільшуватися.
Список літератури:
- Айвазян С.А. Прикладная статистика. Основы эконометрики: Учебник для вузов: В 2 т.– 2-е изд., – Т. 2 / С.А. Айвазян – М.: ЮНИТИ-ДАНА, 2001. – 432 с.
- Балаш В.А., Модели линейной регрессии для панельных данных. Учебное пособие. / В.А. Балаш, О.С. Балаш. – М.: 2002. – 65 с.
- Грешилов А. А., Стакун В. А., Стакун А. А. Математические методы построения прогнозов. — М.: Радио и связь, 1997.- 112 с.
Відомості про авторів:
Іванченко Дар’я Василівна – студентка VI курсу фізико-математичного факультету Кіровоградського державного педагогічного університету імені Володимира Винниченка

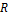
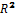 )
)