Ровінський Ярослав

Науковий керівник: канд. т.- н., старший викладач Макарчук О.П.

Кіровоградський державний педагогічний університет імені Володимира Винниченка

Анотація: В статті розглядається побудова і практична перевірка прогностичної сили моделі знаходження прогнозних значень часового ряду на основі многочленів Берштейна.

Ключові слова: многочлени Берштейна, прогностична модель, часовий ряд, регресійна модель, трендова компонента, формозберігаюче наближення, інтерполяція.

Актуальність теми. Многочлени Берштейна, як генератор прогностичної моделі.

Мета роботи. здійснити статистичний аналіз Bernstein polynomials-моделі в контексті інших моделей прогнозування. Для досягнення мети поставлено такі завдання:

1. проаналізувати аналітичну структуру многочленів Берштейна;
2. здійснити статистичний аналіз Bernstein polynomials-моделі по відношенню до степеневої регресійної моделі;
3. здійснити статистичний аналіз Bernstein polynomials-моделі для часового ряду з виділеною трендовою компонентою;

Поліноми Бернштейна — алгебраїчні поліноми, що є лінійною комбінацією  базисних поліномів Бернштейна. Названі на честь українського математика Сергія Натансоновича Бернштейна, який вперше їх вивчав у зв'язку з доведенням теореми Вейєрштрасса [3].

Поліноми Берштейна мають вигляд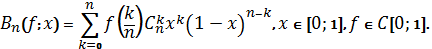  

Поліноми широко використовуються у обчислювальній математиці, теорії ймовірностей, комп'ютерній графіці, зокрема для визначення кривих Без'є.

З поліномами Берштейна пов’язано чимало проблем (дослідження асимптотичних властивостей збіжності, дослідження асимптотичних властивостей коефіцієнтів, побудова швидких алгоритмів зведення полінома Берштейна до канонічного виду тощо) однак важливо те, що вони забезпечують формозберігаюче наближення (Save Preserving Aproximation).

Поліноми Берштейна є генератором нової системи прогнозування, яка вперше розглянута в цій роботі. В подальшому відповідну систему прогнозування будемо називати Bernstein polynomials-модель (Bernstein polynomials – поліноми Берштейна).  

Відповідна прогностична модель будується за наступним алгоритмом. Розглянемо часовий ряд , відповідні значення якого позначимо як .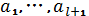

Перш за все нам потрібно згенерувати, яку неперервну функцію на основі відповідного ряду. Нехай 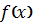 лінійне сплайно, яке утворюється послідовним з’єднанням точок 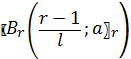. Тобто,  .

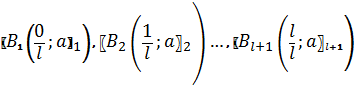Пам’ятаємо, що рівняння прямої, яка проходить через точки 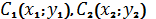 має вигляд: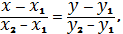 

або в спрощеному вигляді: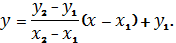 

Аналітична формула для лінійного сплайна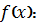 

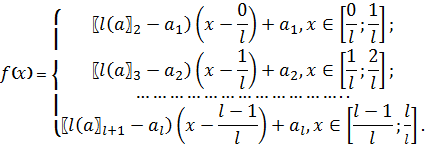
Порівнювались 4 методи прогнозування:

1.Поліном Берштейна 3 степеня;

2.Поліном Берштейна 5 степеня;

3. Лінійна регресія;

4. Квадратична регресія;

В подальшому ми будемо прогнозувати індекс Доу-Джонса в період з 12.2015  по 11.2016 .  Промисло́вий і́ндекс До́у-Джо́нса (англ. Dow Jones Industrial Average, DJIA, Dow 30, або неформально Dow Jones чи The Dow) − біржовий індекс цінних паперів (акцій) 30 найбільших американських підприємств, створений у 1896 році редактором The Wall Street Journal і співзасновником Dow Jones & Company Чарльзом Доу.

   Для кожного методу прогнозування рахуємо величину(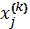− прогноз значення 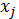по методу  ):  

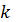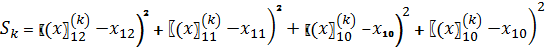
Той метод, якому відповідає найменше значення 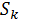 і є найкращим.

В процесі апробації відповідної прогностичної моделі були отримані наступні висновки:

1)      При використанні моделі на основі многочленів по відношенню до регресійної моделі, найкращий результат показала лінійна модель причому найкраща модель серед моделі на основі многочленів, а саме многочлен Берштейна 3 степеня показала гірший результат ніж квадратична регресійна.

2)      При використанні моделі на основі многочленів, з виділеною трендовою компонентою, найкращий результат показала лінійна модель причому найкраща модель серед моделі на основі многочленів, а саме многочлен Берштейна 3 степеня показала кращий результат ніж квадратична регресійна.

3)      Найкращою серед всіх моделей кращою виявилася лінійна модель з виділеною трендовою компонентою, і прогноз індексу Доу-Джонса по ній на 05-11-2016 становить 1821,37.

Список літератури:

1. Бернштейн С. Н. Собрание сочинений. — М., 1954. — Т. 3. — С. 310-348.
2. Виденский B.C. Многочлены Бернштейна. Л.: ЛГПИ им. А.И. Герцена, 1990.
3. Гнеденко Б.В. Курс теории вероятностей. –М.: Наука, 1988. – 448 с.
4. Чистяков В.П. Курс теории вероятностей. – М.: Наука, 1987. – 240 с.
5. Феллер В. Введение в теорию вероятностей и ее приложения. – М.: Мир, 1984. – Т. 1. – 527 с.

Відомості про авторів:

         Ровінський  Ярослав Григорович  – студент VI курсу фізико-математичного факультету Кіровоградського державного педагогічного університету імені Володимира Винниченка.